 |
 |
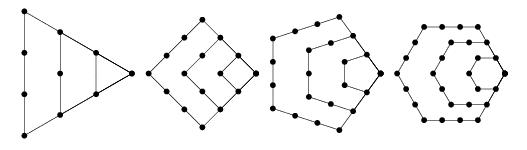
A polygonal number is defined as "A type of figurate number which is a generalization of triangular, square, etc., numbers to an arbitrary n-gonal number. The above diagrams graphically illustrate the process by which the polygonal numbers are built up." (Mathworld.wolfram.com) Every student of school mathematics knows about the square numbers, and many know about the triangular numbers as well. But less familiar are the pentagonal, hexagonal, etc. varieties.
Even less well known is the fact that each of those types of numbers has a cousin of sorts, called the centered polygonal numbers. Yes, the regular triangular numbers have their corresponding "centered" form. The same is true for the squares, pentagonals, hexagonals, etc. (See diagram below.)
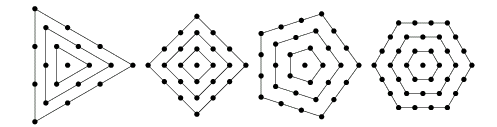
Therefore, our definition for these numbers is "A figurate number in which layers of polygons are drawn centered about a point instead of with the point at a vertex." (Mathworld.wolfram.com)
Many facts and theorems are known about polygonal numbers, especially of the squares and triangulars. We wouldn't be able to talk about the Pythagorean Theorem if it weren't for the squares, just to mention the most famous example of all. And the triangulars arise whenever we are concerned with the sum of consecutive integers, from 1 to n.
What I want to do in this page of WTM is present some ideas that are not normally covered in an average school math class, yet ideas that are well within the understanding of most students. First, we will show the algebraic formulas for both the regular and centered polygonal numbers, up to a level seldom discussed: a 30-sided polygon!
of Sides | form | form |
| n(n + 1)/2 | (3n2 - 3n + 2)/2 | |
| n2 | 2n2 - 2n + 1 | |
| n(3n - 1)/2 | (5n2 - 5n + 2)/2 | |
| n(2n - 1) | 3n2 - 3n + 1 | |
| n(5n - 3)/2 | (7n2 - 7n + 2)/2 | |
| n(3n - 2) | 4n2 - 4n + 1 | |
| n(7n - 5)/2 | (9n2 - 9n + 2)/2 | |
| n(4n - 3) | 5n2 - 5n + 1 | |
| n(9n - 7)/2 | (11n2 - 11n + 2)/2 | |
| n(5n - 4) | 6n2 - 6n + 1 | |
| n(11n - 9)/2 | (13n2 - 13n + 2)/2 | |
| n(6n - 5) | 7n2 - 7n + 1 | |
| n(13n - 11)/2 | (15n2 - 15n + 2)/2 | |
| n(7n - 6) | 8n2 - 8n + 1 | |
| n(15n - 13)/2 | (17n2 - 17n + 2)/2 | |
| n(8n - 7) | 9n2 - 9n + 1 | |
| n(17n - 15)/2 | (19n2 - 19n + 2)/2 | |
| n(9n - 8) | 10n2 - 10n + 1 | |
| n(19n - 17)/2 | (21n2 - 21n + 2)/2 | |
| n(10n - 9) | 11n2 - 11n + 1 | |
| n(21n - 19)/2 | (23n2 - 23n + 2)/2 | |
| n(11n - 10) | 12n2 - 12n + 1 | |
| n(23n - 21)/2 | (25n2 - 25n + 2)/2 | |
| n(12n - 11) | 13n2 - 13n + 1 | |
| n(25n - 23)/2 | (27n2 - 27n + 2)/2 | |
| n(13n - 12)/2 | 14n2 - 14n + 1 | |
| n(27n - 25)/2 | (29n2 - 29n + 2)/2 | |
| n(14n - 13) | 15n2 - 15n + 1 |
Hey! Do you see a pattern in the table? If you do, perhaps you could write a general formula for it; then you could give the formula for any n-gonal number of either type, without using the table, and even beyond 30 sides.
| Name | ||
| triangular | 1, 3, 6, 10, 15, 21, 28, 36, 45, ... | 1, 4, 10, 19, 31, 46, 64, 85, 109, ... |
| square | 1, 4, 9, 16, 25, 36, 49, 64, 81, ... | 1, 5, 13, 25, 41, 61, 85, 113, 145, ... |
| pentagonal | 1, 5, 12, 22, 35, 51, 70, 92, 117, ... | 1, 6, 16, 31, 51, 76, 106, 141, 181, ... |
| hexagonal | 1, 6, 15, 28, 45, 66, 91, 120, 153, ... | 1, 7, 19, 37, 61, 91, 127, 169, 217, ... |
| heptagonal | 1, 7, 18, 34, 55, 81, 112, 148, 189 | 1, 8, 22, 43, 71, 106, 148, 197, 253, ... |
| octagonal | 1, 8, 21, 40, 65, 96, 133, 176, 225, ... | 1, 9, 25, 49, 81, 121, 169, 225, 289, ... |
| nonagonal | 1, 9, 24, 46, 75, 111, 154, 204, 261, ... | 1, 10, 28, 55, 91, 136, 190, 253, 325, ... |
| decagonal | 1, 10, 27, 52, 85, 126, 175, 232, 297, ... | 1, 11, 31, 60, 101, 151, 211, 281, 361, ... |
Now that we have some numbers, what should we do with them? If I may paraphrase an old popular song by Nancy Sinatra, these numbers are made for adding! So consider this...
We again turn to Mathworld for some vital information: Fermat's Polygonal Number Theorem
In 1638, Fermat proposed that every positive integer is a sum of at most three triangular numbers, four square numbers, five pentagonal numbers, and n n-polygonal numbers. Fermat claimed to have a proof of this result, although Fermat's proof has never been found. Gauss proved the triangular case, and noted the event in his diary on July 10, 1796, with the notation
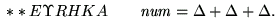
What that little cryptic notation means is that all whole numbers can be expressed as the sum of three, or fewer, triangular numbers. Here is an interesting example:
This illustrates that sometimes a number has two possibilities, with 3 or 2 terms. Nice, huh?
Turning now to the case of the squares... Fermat said that all whole numbers can be expressed as the sum of four, or fewer, square numbers. Let's look at this example:
Notice that there were expressions with 2, 3, and 4 terms. Thereby, arises an interesting idea: given a particular number, how many different expressions can be found? I challenge you to research this and report back to me. Ok?
One more time... For the case of the pentagonals, we can use up to five of them to express all whole numbers. Let's check out the situation for the number 2002.
As before, we have demonstrated that we can achieve our goal with 2-5 terms. In fact, there are many more such ways to do it than presented here. Finding all possible ways is now more difficult, (unless one uses a computer program).
So far we have only been working with the regular polygonal numbers. Let's now look at the centered case. The natural question to ask should be: does there exist an analogue to Fermat's theorem, as discussed above? Specifically, are three CTN's (Centered Triangular Numbers) sufficient to express all whole numbers?
The best way to answer that is to start small and work your way up. Here is a chart for the numbers from 1 to 10. Recall, the set of CTN's is {1, 4, 10, 19, ...}.
Well, I guess that about answers our question, doesn't it? And it didn't take long either.
However, it brings to mind yet another question -- what is the next impossible number?
And the next? And the next?
Then what happens when this idea is extended to CSN's (Centered Square Numbers) and CPN's (Centered Pentagonal Numbers)? What are the impossible values when using these other sets of numbers? And beyond?
[Remember: you can use up to 4 CSN's and 5 CPN's, and so on, in the expressons.]
Another popular activity when one is faced with a long list of numbers is to search for the presence of numbers with special characteristics, such as squares, cubes, or palindromes. Let's first consider the modern favorite of many mathematicians: palindromes.
The "mother of all websites" dealing with palindromes undoubtedly is World!Of Numbers, edited by Patrick De Geest. In his site you can find an extensive treatment of palindromes that are also triangular numbers, and squares as well. In fact, he gives data for the pentagonals up to the nonagonals. We heartily encourage you to visit that site; you will be justly rewarded for your time and efforts.
However, all the data to be found there uses only the regular type of polygonals; there is nothing mentioned about the centered type. Here is our attempt to fill in that gap of trivia information. (Note: At present, our search only shows results up to n = 300 and for k-gonals from k = 3 to 40. We also omit any single-digit palindromes as being trivial in this context.)
While studying the results above, I saw two rather interesting numbers: 1212121 and 1313131. Not only do they share an obvious digital pattern of 1d1d1d1, but they both are the 260th term in their respective orders (k = 36 and 39).
Now if we look back at the 33-gonal and 30-gonal lists, we see 1111111 and 1010101. As one might begin to suspect by now, they are the 260th terms there. So it's table time again!
Also, my friend and colleague from Romania, Andrei Lazanu, sent along some important data regarding the matter above about the impossible cases for numbers to be expressed as the sum of 3, or fewer, CTN's. According to the program he wrote, there are over 70 numbers less than 200 that can not be decomposed in this way. How many can you find? Can you find all of them?
Andrei also was kind enough to provide WTM with some information about how many ways 2002 can be expressed with 5, or fewer, regular pentagonal numbers. It can be done in 166 ways. [See examples above.]
In addition, he informs us that the same task can be achieved in 31 ways with regular triangular numbers, and in 101 ways using regular square numbers. (Thanks, Andrei.)
Next (5/13/02), Andrei has extended the matter of Centered Hexagonal Numbers (CP6N) if ever so slightly...

| Comments? Send e-mail. | Back to top | Go back to Home Page | Go back to Contents |