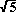 ). This is clearly a shorter distance. Since we are imagining a direct movement of our finger over the printed diagram, in this activity we will use this method.
). This is clearly a shorter distance. Since we are imagining a direct movement of our finger over the printed diagram, in this activity we will use this method.
How "long" is a word? Believe it or not, in the world of Trotter Math that question has two answers. Take, for instance, the word HOUSE. The usual answer is: "it has 5 letters, so that is its length." But if we use the grid of letters shown below, we can obtain a really unique answer: 13.03 units. How is such a value obtained, you ask?
Well, first let's find out how far it is from "H" to "O". There are three ways we could do this:
| Z | ||||
| U | V | W | X | Y |
| P | Q | R | S | T |
| K | L | M | N | O |
| F | G | H | I | J |
| A | B | C | D | E |
- place our finger on H, move 2 spaces to the right, arriving at J, then move up 1 space to the O; or
- place our finger on H, move up 1 space to M, then go 2 spaces over to the O; or
- we could just "go as the crow flies", sort of diagonally direct from H to O.
In the first and second methods, our distance was "3 units". But in the third way, the distance is about 2.24 units (actually 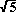 ). This is clearly a shorter distance. Since we are imagining a direct movement of our finger over the printed diagram, in this activity we will use this method.
). This is clearly a shorter distance. Since we are imagining a direct movement of our finger over the printed diagram, in this activity we will use this method.
But how was the value 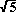 figured, you ask (again)? By the famous Pythagorean Theorem, is the answer. In going from H to O in either of the first two methods, we traveled 2 units horizontally and one unit vertically. These constitute the lengths of the legs of a right triangle, in which the direct H-O distance makes up the hypotenuse. As they say, the "rest is homework".
figured, you ask (again)? By the famous Pythagorean Theorem, is the answer. In going from H to O in either of the first two methods, we traveled 2 units horizontally and one unit vertically. These constitute the lengths of the legs of a right triangle, in which the direct H-O distance makes up the hypotenuse. As they say, the "rest is homework".
HO2 = HJ2 + JO2 = 22 + 12 = 4 + 1 = 5 HO =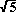
The other four distances are found in a similar manner: OU = 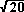 , US =
, US =  , and SE =
, and SE =  . The total distance in "radical form" (as it is called in algebra textbooks) is
. The total distance in "radical form" (as it is called in algebra textbooks) is

which comes out in a calculator as about 13.03 units.
Provide pairs of related words, such as "boy vs. man", "cat vs. dog", "sugar vs. candy", etc.; then compare their lengths, using the "<" and ">" symbols.
An easy way to vary this activity is to change the chart of letters. Here are two samples of what I mean. The first arranges the letters in a zig-zag manner.

While many words will now have different distances as a result of this transformation, some will not! They could be called invariant words.
The second one rotates the dimensions of the chart and employs a circular placement of the letters.

| Comments? Send e-mail. | Back to top | Go back to Home Page | Go back to Contents |